Numerical models reproduce the formation of regular networks of joints/fractures

Joints often form spectacular very regular (parallel or more complex, e.g., orthogonal) networks (Fig. 1) that have major practical importance in the production of economic fluids such as water, gas, and oil.

It is largely for this reason that joints have been objects of numerous studies since a century. According to the conventional wisdom based on « Linear Elastic Fracture Mechanics » (LEFM), these fractures are formed in very brittle rocks by initiating from the preexistent defects/heterogeneities that are stress concentrators. The regularity (i.e., parallelism) of natural joints, on the contrary, suggests that they form in rather uniform both material and stress field.

Unfortunately, one cannot observe, study, and hence, know the conditions and evolution of natural jointing. But it was possible to investigate this processes in the original laboratory experiments where joints and their regular networks were obtained in homogeneous Rock Analogue Granular Material, GRAM (Fig. 2).

These experiments have revealed that the formation of a fracture in stricto sensu (having open space between its borders) is preceded by the localization of inelastic deformation or damage within a band, oriented normally to σ₃ and having ta hickness of several grain sizes. The porosity within the band is increased (the material is dilated) and its strength is reduced.

A fracture results from the evolution of this dilation band. This evolution was difficult to constrain experimentally and remained not understood. On the other hand, according to the dominant paradigm (LEFM), the fracture (rupture) of rock follows directly the elastic deformation. It is supposed to occur within a very small zone (within a « point ») at the tip of the preexistent flaw leaving no possibility for the formation of a band of damaged (inelastic deformed) material. The uncertainty caused by the contradiction between the classical ideas and the experiential results had to be removed by proposing a physical explanation of these results.

It took years of experimental studies, theoretical developments, and numerical simulations to develop a new approach to the mechanism of jointing. In its last paper, Alexandre Chemenda presents experimental results showing that fracturing of very brittle geomaterials is preceded and accompanied by a non-negligible inelastic deformation that should be taken into account in the theoretical models of jointing. It was found, that this deformation is necessary for structuring/formation of the regular networks of joints.

A new constitutive model has been formulated that describes both shear and tensile failure (damage) mechanisms coupled by simultaneous evolution of both shear and tensile, σ_t, strengths with deformation. The numerical models run within this constitutive framework correspond to three sedimentary layers deformed under horizontal extension and constant lithostatic pressure (or depth), Fig. 3 (as in the experimental models in Fig. 2).

Fracturing started with diffuse damage of the central layer, which then was localized within a dense network of pure dilation deformation bands emanating from the layer interfaces (Fig. 4a, 2nd column). Some bands have cut the entire layer, whereas others were abandoned at different stages of their evolution (Fig. 4, 2nd column). The damage leads to a progressive failure of the material within the bands resulting in a decrease of the tensile strength σ_t (Fig. 4, 1st column).

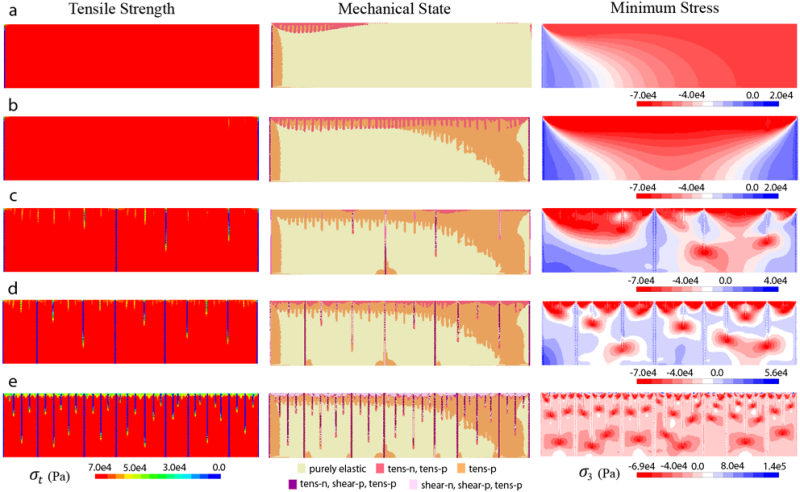
At stages a and b, the bands are already initiated (Fig. 4, 2nd column), but the reduction of σ_t is too small to be visible. Fractures are initiated within the bands when the material is completely broken and σ_t becomes zero. This strongly perturbs the stress field which evolves with the bands/fracture evolution (Fig. 4, 3rd column). Both the length and thickness of the bands are proportional to the material ductility which varies in the models. As indicated, the evolution of some bands stops at different stages and they never become fractures. Such bands belonging to the network of natural orthogonal joints in an outcrop of dolomicrite were discovered by J.-P. Petit. All fractures emanating from the horizontal interfaces of the layer do not completely cut through it (Fig. 4e). This also is the case in the experimental models (Fig. 2) and in the natural examples.

            The presented work (based on the experimental, geological, theoretical, and numerical studies) and the approach developed for addressing the formation of joints enable practical applications by modeling the fracturing of complex 3-D structures in geological reservoirs.